Turbulence and Society
Understanding Social Movements through the Lens of Fluid Dynamics
Big whirls have little whirls,
Which feed on their velocity;
And little whirls have lesser whirls,
And so on to viscosity.
- L. F. Richardson

The quote above was in the textbook used in my turbulence class in graduate school. It was striking to me, at first. The poetry of this verse juxtaposed the abstract symbols and equations that I had gotten used to in college. This juxtaposition continued throughout the class. There were graphs, equations, and new variables just like all other classes, but there was an added mystical quality to turbulence. Turbulent air follows the same equations as non-turbulent (laminar) air, but it is necessary to look at much smaller sections of a flow to calculate it exactly. My professor noted that if one were to try to simulate a turbulent flow down to the molecular level, one would need a domain the size of our galaxy. In short, it’s impossible to perfectly predict turbulence. Beyond that, it is incredibly difficult to predict when and where flows will become turbulent. This remains a very active branch of fluid mechanics research, especially in hypersonics.
Lewis Fry Richardson was a pioneer meteorologist whose methods are still used today. When he proposed a numerical method to solve differential equations, there were not enough computers (human or machine) available to complete the process. It was in the book that explains this process, Weather Prediction by Numerical Process, where Richardson wrote the above quote. His work continued into the realm of atmospheric turbulence which gave rise to a non dimensional number named after him, thus placing him among scientific royalty. Richardson went beyond fluid mechanics in some of his work as well. In his posthumously published Statistics of Deadly Quarrels, he attempted to combine politics and probability to create a new field, quantitative history and found that it
is not at present cultivated under the auspices of any one learned society; indeed it falls between two stools, because the historians and other students of human nature, are in general strongly adverse from mathematics, whereas the mathematicians are apt to regard politics and history as incalculable.
In his work he was able to find connections between some nations and religions and their respective pacifism or bellicosity. Most of the findings were not significant, though.
While, I find grand theories of history lacking, I can’t help but to find Richardson’s work interesting. The quote was serendipitous as it led me to see (or create) similarities between us. Namely we both studied fluid mechanics and have an interest in history. To my knowledge, there are no other similarities, but I’ll take what I can get. I was a bit disappointed in his research path, though. I feel that there is a connection to be made between the study of turbulence and the study of human conflict. I will now become a bit of a hypocrite and try to smash these two discordant ideas into a singular theory.
Turbulence
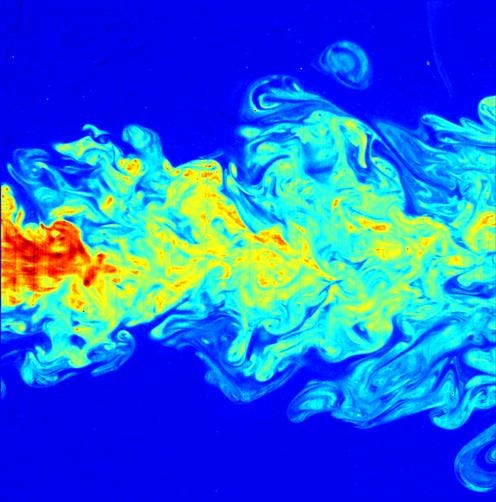
Turbulence at its core is a chaotic flow. It contrasts laminar flow, the orderly sibling. It whips and spins unpredictably, rapidly mixing the air together. This mixing can be great when trying to mix air and fuel in jet engines. But it can also be damaging when trying to re-enter from space, as temperatures in turbulent flows reach about three times higher than in laminar. I don’t want to go down the rabbit hole of turbulence research, so I will instead take the quote and break it down. We’ll start after turbulence is induced and then look at how it is induced in the first place.
Big whirls have little whirls
The “big whirls” here are the eddies you can see most prominiently in turbulent flows. In the image above, they are the swirls that emanate from the back of the sphere. Within these larger swirls are smaller ones, harder to distinguish. They merge and separate, seemingly at will. Despite the above image, turbulence is chaotic. It does not have a defined structure or rhythm.
These big whirls are grand social movements. These are revolutions, rebellions, civil unrest. Throughout history these movements come and go, merge and separate, sometimes without clear reasoning. Within broader movements there are smaller ones and so on.
Which feed on their velocity;
In turbulence there is an idea called the energy cascade, first proposed in 1922 by L. F. Richardson. The amount of energy is constant in any given system. This is a fundamental rule of the universe. So these lesser whirls have less energy than the larger ones on their own. Furthermore, they are created and “feed” off of the kinetic energy, the velocity, of the bigger whirls.
In social movements, the ability for smaller groups to form is dependent on the energy, the total clout, of the larger movement. These don’t all have to be radical. Some continue down the path of the greater movement, others buck the trend. As these groups get smaller and smaller, they get harder to see throughout history.
And little whirls have lesser whirls,
See above, only smaller.
The smaller groups have their individuals; their dynamic duos. These people would not exist if not for the energy cascade. They would have no energy themselves if it was not transferred down to them. It is also here that one finds the lowly workers trying to get by in the new world, changed forever from this turbulent period.
And so on to viscosity.
At the smallest scale of turbulence, the so-called Kolmogorov scale, is where the viscosity of the fluid (how thick it is) matters. It is here that the energy is dissipated. The kinetic energy is thus converted to heat. The energy is not lost, but it has less ability to make further change.
Once the social movement reaches the individual, most are ready to put down the sword and pick up the shovel. The fervor of before is converted into building a new society, or rebuilding the old one.
All of these steps occur once a flow has become turbulent, but how does it get there in the first place?
Induction
The creation of a turbulent flow is well understood to an extent. It is known that the ability for a flow becomes turbulent is related to its Reynolds number, the higher it is, the more likely it will be turbulent1. We also know it can be induced by rapid changes in temperature and velocity in a fluid. This can be done by introducing heat or higher speed gasses. It is also understood that disturbances, like the roughness of a surface or a large obstruction on a wing, can induce turbulence. However, the chaotic nature of turbulence does not allow the formation, or total energy, or exact structure to be predicted. The same test can often give vastly different results. Furthermore, simulations rarely match reality.
To me, our understanding of inducing turbulence can be mapped to revolutionary movements in history. They are not easily predicted in scale or scope. The same inputs need not lead to the same outputs. But, there are patterns that repeat in history. Perhaps that is just a culmination in innate human ability to find them, or, like in turbulent flows, the properties of the society or the outsized influence of a single person can lead to social upheaval.
I have stated that I don't like the Great Man Theory or the idea of societal determinism. They interconnect, much like turbulent flows. The large movements can influence down. All the same, disturbances at the molecular level can induce turbulence into a system. By 1670, the British colonial world was ripe for a disturbance to have an outsized impact.
Turbulence in History
In Massachusetts, and the rest of New England, the continuous growth of towns and settlements pushed the Natives further and further from the coast. Minor skirmishes, raids, and cattle killing instilled a lack of trust between the English and the Natives. The trade of guns and alcohol created a chaotic environment throughout the region. When this trade and the relative peace ended on the death of Massasoit, the seeds were sown for a major conflict. But it wasn’t until Metacom, also known as Philip by the English, came to power that it reached a breaking point. Philip wasn’t the sole reason King Philip’s War occurred. He did take an active role though. He stockpiled weapons and built alliances. So, when a trial found the murderers of a Praying Indian, John Sassamon, guilty, the spark was lit and war was on. But Philip was not really prepared to be a war leader. Nathaniel Philbrick states it like this:
By the end of the month, both [Josiah] Winslow and Philip had become victims of their own rhetoric and posturing. Paralyzed by worry and wishful thinking, they were powerless to restrain what years of reckless greed, arrogance, opportunism, and ineptitude had unleashed among the young warriors of the Pokanokets2.
In Virginia, the divide between the planters and the servants grew steadily after the Third Anglo-Powhatan war. Servants, even after being freed from bondage, were in no position to buy land. They would often end up working someone else’s land by renting or under a new contract of indenture. The profits from tobacco began to dwindle so planters continuously increased the labor force to try to make up for it. The colonial government was made up entirely by the upper strata, so the servants found no solace there. Nathaniel Bacon was a planter himself, but his grievances against the government mirrored the servants. So, when he took matters into his own hands after a series of Susquehannock raids, the servants were ready to back him. But he likely was not trying to start a class war. Edmund S. Morgan states:
Beginning as a crusade against the Indians, who proved elusive targets, it ended in a series of plundering forays against those who had stuck with Berkeley…Bacon had probably never intended it to turn into a rebellion3.
Philip took more of a back seat in his named conflict than did Bacon. Bacon himself was only alive for the first half of the revolt, before being replaced by Joseph Ingram. But, in the end, towns were burned, people were killed, and Anglo-Indian relations were shattered. The people that make the difference in society are not necessarily those that wield a flamethrower. Sometimes all they do is cast a spark. But like in turbulent flows, the end result is the same.
The Reynolds number is a non-dimensional number comparing the viscous forces to the inertial forces of a flow.
The higher the viscosity (i.e. thicker liquid), the lower the chance of turbulence. Conversely, the higher the velocity, the more likely it will go turbulent. This is obviously a vast oversimplification, but it will do for this essay.
Nathaniel Philbrick. Mayflower: A Story of Courage, Community, and War. pp. 224
Edmund S. Morgan. American Slavery, American Freedom. pp. 269